Este documento contiene una breve explicación acerca del calculo integral,espero que sea de tu utilidad.
jueves, 29 de noviembre de 2012
domingo, 25 de noviembre de 2012
PROBLEMA DE LA CAJA 40X30
El siguiente vídeo nos muestra como resolver un problema acerca del tema máximos y mínimos... solo da click en el siguiente link:
http://www.youtube.com/watch?v=r6XrzkkQwF0&feature=youtu.be
En la siguiente presentación describe el procedimiento que se llevo a cabo para resolver el problema:
En la siguiente presentación describe el procedimiento que se llevo a cabo para resolver el problema:
lunes, 19 de noviembre de 2012
Aplicación de la derivada 7

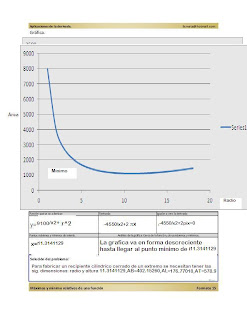
Se desea fabricar un recipiente cilíndrico sin tapa con capacidad de 4550 litros. ¿Cuales deben ser sus dimensiones para que el material utilizado sea el mínimo posible?
Los siguientes formatos muestran la solución del problema:
Para hacer el siguiente formato mencionamos el radio como "x" y la altura 4550/pi(radio al cuadrado) y lo sustituimos en la formula de Área Total, así: 2(pi)(x)(4550/(pi)(x al cuadrado)+(pi)(x al cuadrado).
Aplicación de la derivada 6
Se desea fabricar un recipiente cilíndrico sin tapa con capacidad de un litro (1000 cm3). ¿Cuales deben ser sus dimensiones para que el material utilizado sea el mínimo posible?
En los siguientes formatos esta la solución del problema:
Para entender el siguiente formato nombramos al radio como "X" y la altura 1000/pi(radio al cuadrado) lo sustituimos en la formula del área total, así: 2(pi)(x)(1000/(pi)(radio al cuadrado)+(pi)(x al cuadrado).
Aplicacion de la derivada 5
Se desea cercar un terreno rectangular, tomando como uno de los
lados, una barda previamente construida. Se dispone de material
suficiente para construir 2002 metros cerca. ¿Cuales deben ser las dimensiones
del terreno para que el área cercada sea la máxima posible.
En esta pagina hay un problema muy similar al que nosotros
haremos, analizalo paso a paso para que entender mejor nuestro
problema.
La siguiente presentación sera de
utilidad para plantear nuestro problema:
Aplicación de la derivada 4
Se desea cercar un terreno rectangular, tomando como uno de los lados, una barda previamente construida. Se dispone de material suficiente para construir 135 metros cerca. ¿Cuales deben ser las dimensiones del terreno para que el área cercada sea la máxima posible.
En esta pagina hay un problema muy similar al que nosotros haremos, analizalo paso a paso para que entender mejor nuestro problema.
http://licmata-math.blogspot.mx/2012/11/problema-resuelto-de-maximos-y-minimos.html
La siguiente presentación sera de utilidad para plantear nuestro problema:
El problema resuelto esta en los siguientes formatos:
Saludos =)
domingo, 18 de noviembre de 2012
Aplicaciones de la derivada 3
Se dispone de una pieza rectangular que mide 820x740, con este material se desea fabricar una caja sin tapa. Para ello se recortaran 4 cuadrados, uno en cada esquina y se doblara la pieza resultante. ¿Cuanto deben medir los cuadrados que se recortaran para que el volumen de la caja resultante sea el máximo posible?
En esta pagina hay un problema muy similar al que nosotros haremos, si gustas analizarlo para entender mejor nuestro problema:
La siguiente presentación sera de nuestra utilidad para poder plantear nuestro problema:
Aplicaciones de la derivada Maximizar volumen (Maximize volume) from Matematica de Samos
El problema resuelto esta en los siguientes formatos:
El problema resuelto esta en los siguientes formatos:
Saludos
Aplicaciones de la derivada 2
Se dispone de una pieza rectangular que mide 80x70, con este material se desea fabricar una caja sin tapa.Para ello se recortaran cuatro cuadrados, uno en cada esquina y se doblara la pieza resultante. ¿Cuanto deben medir los cuadrados que se recortaran para que el volumen de la caja resultante sea el máximo posible?
En esta pagina hay un problema resuelto muy similar al que nosotros haremos, si gustas analizalo para entender mejor nuestro problema.
http://licmata-math.blogspot.mx/2012/11/problema-resuelto-de-maximos-y-minimos.html
La siguiente presentación sera de tu utilidad para poder plantear nuestro problema.
Aplicaciones de la derivada Maximizar volumen (Maximize volume) from Matematica de Samos
El problema resuelto está en los siguientes formatos:
El problema resuelto está en los siguientes formatos:
Saludos
sábado, 17 de noviembre de 2012
Aplicaciones de la Derivada 1
Se dispone de una pieza rectangular que mide 40x30, con este material se va a fabricar una caja sin tapa, para ello se recortaran cuatro cuadrados, uno en cada esquina y se doblara la pieza resultante.
¿Cuanto deben medir los cuadrados que se recortaran para que el volumen de la caja resultante sea el máximo posible?
Problema ya resuelto en el blog:
La presentación que contiene el planteamiento es:
Aplicaciones de la derivada Maximizar volumen (Maximize volume) from Matematica de Samos
Y el problema resuelto en el formato es:
Y el problema resuelto en el formato es:
domingo, 11 de noviembre de 2012
Problema de Razonamiento con tres incognitas
Problema acerca de los modelos de televisiones
A continuación se presenta un
problema de Razonamiento con tres incógnitas en la
siguiente presentación de Power Point. En esta presentación
explicare paso a paso el problema para que entendamos e identifiquemos lo que
nos esta pidiendo el problema.
Para
solucionar el problema tenemos que tener claro los datos que tenemos y los que
nos están pidiendo, por eso este FORMATO te sera de utilidad para
que aquí los ordenes.
Existen
muchos métodos para resolver sistemas de ecuaciones con
tres incógnitas, en este caso obtendremos los valores de x1, x2 y x3 a través del método de
cramer. A continuación aparece una hoja de calculo donde lo único que tienes
que hacer es introducir los valores de tus ecuaciones para resolverlas.
Después de obtener los valores de x1, x2 y x3 mediante la hoja de Excel, necesitamos sustituirlos en nuestras ecuaciones para solucionar el problema.
x1+x2+x3=2400
(675)+(1150)+(575)=2400
Televisores modelo 19" x1= 675
Televisores modelo 21" x2=1150
Televisores modelo 27" x3=575
Espero y este problema de tres incógnitas te haya ayudado a comprender de mejor manera la resolución del problema.
Problema de Razonamiento con tres incógnitas.
Problema de los boletos del concierto de Mana
A continuación se presenta un problema de Razonamiento con tres incógnitas en la siguiente presentación de Power Point. En esta presentación explicare paso a paso el problema para que entendamos e identifiquemos lo que nos esta pidiendo el problema.
Para solucionar el problema tenemos que tener claro los datos que tenemos y los que nos están pidiendo, por eso este FORMATO te sera de utilidad para que aquí los ordenes.
Existen muchos métodos para resolver sistemas de ecuaciones con tres incógnitas, en este caso obtendremos los valores de x1, x2 y x3 a través del método de cramer. A continuación aparece una hoja de calculo donde lo único que tienes que hacer es introducir los valores de tus ecuaciones para resolverlas.
Una vez sabiendo los valor de x1, x2 y x3 tenemos que sustituirlos en nuestras ecuaciones para obtener la solcuion del problema
300X1+ 700X2+1300X3=
7,390,000
300(2550)+700(5100)+1300(2350)=7,390,000
Se vendieron en total 2550+5100+2350=1000 boletos
Boletos general=2550
Boletos numerados=5100
Boletos vip=2350
Problema de razonamiento con dos incógnitas.
Problema de mezclas
A continuación se presenta un problema de dos incógnitas en la siguiente presentación de Power Point. En esta presentación explicare el problema paso a paso para que entendamos e identifiquemos lo que nos esta pidiendo el problema.
Para solucionar el problema tenemos que tener muy claros los datos que tenemos y los que no están pidiendo por eso este FORMATO te sera de utilidad para que aquí los ordenes.
Existen muchos métodos para resolver sistemas de ecuaciones con dos incógnitas, en este caso obtendremos los valores de "x" y "y" a través del método gráfico.A continuación aparece una hoja de Excel donde lo único que tienes que hacer es introducir los valores de tus ecuaciones para resolverlas.
Una vez sabiendo los valores de "x" y "y" tenemos que sustituirlos en nuestras ecuaciones para saber la solución del problema.
x - y = -16
37.33 - 53.33= -16
Kilogramos de chocolates que cuestan $15 x= 37.33
Kilogramos de chocolates que cuestan $18 y= 53.33
Espero y sea de tu utilidad este material, saludos =)
Problema de Razonamiento con dos incógnitas.
Problema de distancias
A continuación se presenta un problema de razonamiento de dos incógnitas en la siguiente presentación de Power Point . En esta presentación explicare el problema paso a paso para que lo entendamos y podamos identificar los datos que nos ayudaran a formular las ecuaciones del problema.
Para solucionar el problema tenemos que tener muy claros los datos que tenemos y lo que nos están pidiendo, por eso el siguiente FORMATO te será de utilidad para que aquí los ordenes.
Existen muchos métodos para resolver ecuaciones con dos incógnitas, en este caso obtendremos los valores a través del método gráfico que se presenta en la siguiente hoja de Excel, lo único que debes hacer es introducir los valores de tus ecuaciones.
Una vez sabiendo los valores de "x" y "y", tenemos que sustituirlos en nuestras ecuaciones para saber la solución del problema.
x - y = -16
Velocidad en tramo lluvioso x= 80
Velocidad en tramo despejado y= 96
4.5x+8.75y=1200
4.5(80)+8.75(96)=1200
Distancia tramo lluvioso 4.5(80)=360
Distancia tramo despejado 8.75(96)=840
Espero y sea de tu utilidad este material, saludos
domingo, 28 de octubre de 2012
Sistema de ecuaciones 7x7
Esta hoja de calculo te servirá para resolver problemas de siete ecuaciones con siete incógnitas..
Sistema de ecuaciones 6x6
Esta hoja de calculo te ayudara a resolver problemas de seis ecuaciones con seis incógnitas, podrás analizar el procedimiento para comprobar tus resultados......
sábado, 27 de octubre de 2012
Sistema de ecuaciones 5x5
A continuación este libro de excel te sera de utilidad para encontrar los valores de tus ecuaciones con cinco incógnitas,ojala sea de tu ayuda =)
Sistema de ecuaciones 4x4
Esta hoja de calculo te sera útil para resolver problemas de cuatro ecuaciones con cuatro incógnitas, lo único que debes hacer es remplazar las cantidades que hay en la hoja de calculo por las cifras de tus ecuaciones...
Sistema de ecuaciones 3x3
A continuación aparecerá una hoja de excel que te ayudara a resolver problemas de tres ecuaciones con tres incógnitas, lo único que debes hacer es introducir los valores de tus ecuaciones.
domingo, 21 de octubre de 2012
Método gráfico
Método gráfico
Existen muchos métodos para resolver sistemas de ecuaciones con dos incógnitas, uno de ellos es el método gráfico.
El método gráfico consiste en representar en el plano cartesiano las ecuaciones para determinar el punto de intersección a través de la observación, las coordenadas que señalen el punto de intersección serán los valores de "X" y "Y".
A continuación esta hoja de excel te ayudará a resolver ecuaciones con dos incógnitas.
<iframe width="600" height="450" frameborder="0" scrolling="no" src="https://r.office.microsoft.com/r/rlidExcelEmbed?su=-7902177577968539739&Fi=SD9255D35C4120E7A5!223&ak=t%3d0%26s%3d0%26v%3d!ACM4Rf_FRo5QwZE&kip=1&wdAllowInteractivity=False&wdHideGridlines=True&wdHideHeaders=True&wdDownloadButton=True"></iframe>
Suscribirse a:
Comentarios (Atom)